Uma abordagem neural para estimação de conjugado em motores de indução
Alessandro GoedtelI; Ivan N. da SilvaI; Paulo J. A. SerniII
IUSP / EESC / SEL, Av. Trabalhador Sancarlense, 400 Centro, CEP 13566-590, São Carlos - SP
IIUNESP / FE / DEE, Av. Luis Edmundo Coube, S/N CP 473, CEP 17033-360, Bauru - SP
IIUNESP / FE / DEE, Av. Luis Edmundo Coube, S/N CP 473, CEP 17033-360, Bauru - SP
RESUMO
Os motores de indução são utilizados nos mais diversos setores industriais. Entretanto, a seleção de um motor de indução em determinada aplicação é imprecisa nos casos em que não há conhecimento do comportamento da carga que está acoplada ao eixo do motor. A proposta deste trabalho é fornecer uma ferramenta alternativa aos métodos tradicionais de identificação usando as redes neurais artificiais. O potencial desta proposta está em sua facilidade de implementação em hardware, tendo em vista que a metodologia não necessita de sensores de torque, assim como não requer alto poder computacional. Resultados de simulação são apresentados para validar a proposta.
Palavras-chave: Motores de indução, modelagem de cargas, redes neurais artificiais, estimativa de parâmetros, identificação de sistemas.
ABSTRACT
Induction motors are widely used in several industrial sectors. However, the selection of induction motors is often inaccurate because, in most cases, the load behavior in the shaft is completely unknown. The proposal of this paper is to use artificial neural networks as a tool for dimensioning induction motors rather than conventional methods, which use classical identification techniques and mechanical load modeling. The potential of this approach is the simple hardware implementation since the methodology does not require torque sensor nor powerful computational processors. Simulation results are also presented to validate the proposed approach.
Keywords: Induction motors, load modeling, neural networks, parameter estimation, system identification.
1 INTRODUÇÃO
Motores de Indução Trifásicos (MIT) são usados em muitos setores industriais nos quais a conversão de energia elétrica em mecânica motriz se faz necessária. O uso extensivo deste motor está frequentemente associado com suas características construtivas robustas, fácil manutenção, adaptação a diversas situações de cargas e operação econômica quando bem dimensionado. Entretanto, quando o comportamento da carga é desconhecido, a seleção do MIT apropriado a uma determinada atividade torna-se uma tarefa difícil, uma vez que a prática usual é experimentar um motor na aplicação específica. Se numa experimentação em particular o motor apresenta medidas de corrente com valor acima do nominal e velocidade abaixo do valor admissível, a escolha deste motor mostra-se inadequada. O próximo passo, nesta sistemática, é a substituição deste motor por outro, normalmente com maior potência em relação ao primeiro.
Demonstrações matemáticas e práticas comprovam que um MIT, o qual trabalha de forma superdimensionada apresenta redução do seu fator de potência e diminuição de sua eficiência (Fitzgerald et. al., 1975; Kosov, 1972). Por outro lado, quando o MIT estiver trabalhando de forma subdimensionada o mesmo apresenta sobreaquecimento e uma drástica redução em sua vida útil (Kosov, 1972).
Uma pesquisa feita pela CEMIG (Companhia Energética de Minas Gerais) com 3425 motores de indução trifásicos, em diversos setores industriais, mostrou que 28,7% destes motores trabalhavam de forma superdimensionada enquanto 5,9% estavam operando de forma subdimensionada. Um outro estudo, realizado pela COPEL (Companhia Energética do Estado do Paraná) com 6108 motores de indução trifásicos, mostrou que 37,75% estavam trabalhando de forma superdimensionada (Marach, 2001).
A estimativa de conjugado de carga de motores de indução tem três objetivos principais. O primeiro, e mais importante, é prover informações sobre a carga contribuindo para o correto dimensionamento do motor em determinada aplicação. O segundo objetivo é prover dados relativos ao comportamento da carga no eixo de forma a determinar a eficiência e performance da conversão de energia (El-Ibiary, 2003). Em terceiro lugar, a estimativa de conjugado aplicada nos eixos dos motores de indução é de fundamental importância para o desenvolvimento de técnicas eficientes de controle do motor de indução no regime transitório e permanente (Vas, 1998; Vas, 1999).
Conforme Marino et. al. (2004) o controle dos motores de indução são difíceis por diversas razões: a dinâmica é intrínsecamente não linear e multivariável, não são todas as variáveis de estado nem todas as saídas que estão disponíveis para retro-alimentação onde há parâmetros críticos como resistências e conjugado de carga os quais mudam durante a operação.
No trabalho de Murat et. al. (2004), o qual aborda a técnica de Controle Direto de Torque (CDT), menciona que a falta de informação relativa ao conjugado de carga e incertezas relativas as resistências de rotor e estator constituem o grande desafio para o desempenho destes sistemas. Ainda, os autores mencionam que no Controle Vetorial (CV) de alto desempenho para o motor de indução o qual utiliza técnicas sensorless, é essencial conhecer a temperatura, varição de resistências de rotor e estator e sua dependência com a frequência de chaveamento além do conjugado de carga.
O artigo de Boulter (2004) aborda a escolha de um sistema de acionamento adequado para uma aplicação onde o conjugado exigido pela carga é crítico. Neste trabalho é apresentado um exemplo onde o mapeamento das características torque versus velocidade é feito por um sistema de acionamento e controle (driver). O autor sugere a realimentação do sinal de conjugado através de células de carga para superar (e melhorar) o desempenho do driver devido as não linearidades presentes no mapeamento de torque versus velocidade. Este artigo pode contribuir com o trabalho de Boulter (2004), uma vez que substitui o uso de sensores por um estimador baseado em redes neurais artificiais.
Neste sentido, este trabalho contribui com os trabalhos de Marino et. al. (2004), Murat et. al.(2004) e Boulter (2004), entre outros, os quais abordam o controle do motor de indução, pois estima o conjugado de carga, do transitório ao regime permanente.
Os métodos convencionais para determinação do conjugado de carga, do transitório ao regime permanente, são baseados em técnicas diretas e indiretas. As técnicas diretas consistem no uso de medidores de torque girantes (torquímetros) acoplados entre o motor e a carga. De acordo com Britto (1994), o uso destes dispositivos de medida exigem deslocamento longitudinal entre o motor e a carga. A desvantagem associada ao uso de torquímetros girantes reside no fato de algumas cargas exigirem alto conjugado de partida, implicando num superdimensionamento do elemento sensor e reduzindo assim sua sensibilidade. Além disso, os torquímetros devem ser alinhados de forma cuidadosa com o objetivo de evitar flexões no eixo e conseqüente redução de sua vida útil, agregando desta forma alto custo ao procedimento de instalação.
As técnicas indiretas para determinação do conjugado de carga, por sua vez, são baseadas em modelos matemáticos que representam a dinâmica eletromagnética do motor em relação a carga (Chen e Sheu, 2002; Sheu e Chen, 1999). O uso destas técnicas permite a estimativa do conjugado, do transitório ao regime permanente, através da solução de sistemas de equações diferenciais. A resolução destas equações depende do conhecimento de diversos parâmetros elétricos e mecânicos do motor, tais como a resitência do rotor e estator, as indutâncias de magnetização, entre outros. Entretanto, a obtenção destes parâmetros num ambiente industrial pode ser uma tarefa árdua e complicada. Além disso, os algoritmos para implementação de tais modelos exigem altas taxas de processamento para aplicações de tempo real (Huang et. al., 1999).
Com o objetivo de superar estas dificuldades, alguns métodos para estimativa de conjugado baseados em modelos dinâmicos linearizados foram desenvolvidos (Ong, 1997; Fitzgerald et. al., 1975; Kosov, 1972; El-Ibiary, 2003). Entretanto, estes modelos estimam o conjugado de carga apenas no regime permanente. A dificuldade de implementação destes modelos em hardware, a falta de precisão devido a linearização do modelo e a falta de parâmetros elétricos e mecânicos do motor pode fazer com que a implementação em aplicações de tempo-real seja uma tarefa difícil. Outros métodos para estimativa de conjugado, tais como os baseados em observadores de estado e observadores de modo deslizante, foram desenvolvidos particularmente para aplicações de controle e não com o objetivo de dimensionamento de motores (Krzeminski, 1999; Proca et. al., 2003).
Recentemente, diversos trabalhos usando redes neurais artificiais têm mostrado resultados promissores na solução de problemas envolvendo o controle dos motores de indução (Chen e Sheu, 2002; Lin e Way, 2002; Huang et. al., 1999; Sheu e Chen, 1999; Bharadwaj et. al., 2004). Este trabalho, diferentemente dos citados acima, propõe uma estimativa eficiente para conjugado baseada em redes neurais artificiais. A presente proposta, em contraste com os métodos baseados em modelos dinâmicos linearizados, tem a capacidade de estimar o conjugado do transitório ao regime permanente.
A maior vantagem das Redes Neurais Artificiais (RNA) está baseada na habilidade em aproximar relações não-lineares (Haykin, 1999). Quando as RNA são implementadas para estimar conjugado de carga a resolução de complexas equações não lineares, a modelagem matemática rigorosa e os erros de modelagem são evitados. As não linearidades envolvidas com a estimativa de conjugado estão implícitas nos pesos sinápticos da rede. Desta forma, as RNA podem ser vistas como um método para identificação não linear adaptativo, através da identificação de padrões no processo de estimativa do conjugado. Conforme Narendra e Parthasarathy (1990) o uso das redes neurais é factível para identificação e controle de sistemas dinâmicos não lineares.
As potenciais contribuições da proposta apresentada neste trabalho são: i) uso de sensores relativamente simples de implementar como tensão, corrente e velocidade os quais são as entradas do sistema, ii) reduzido poder de processamento necessário para estimativa de conjugado, uma vez que as RNA (após treinadas) se reduzem a simples cálculo matricial e iii) a metodologia proposta não necessita de resolução de sistemas de equações diferenciais e nem dos parâmetros elétricos da máquina na aplicação no campo.
Desta forma, este trabalho propõe o uso de redes neurais artificiais como um método eficiente na estimativa do conjugado em motores de indução, com o objetivo de melhorar o dimensionamento para essa classe de motores e auxiliar na otimização dos sistemas de controle, cuja variável de interesse é o conjugado, além da predição de falhas mecânicas nos sistemas envolvidos. Ressalta-se ainda que o método proposto realiza estimações estáticas do torque, considerando que é conhecido o momento de inércia e o tipo da carga. A proposta tem também grande potencial para aplicação industrial, uma vez que verifica o dimensionamento do motor e auxilia na determinação da melhor estratégia de acionamento da carga frente a uma aplicação em particular.
2 ASPECTOS DA MODELAGEM MATEMÁTICA DO MOTOR DE INDUÇÃO
O primeiro passo envolvido no ajuste dos pesos sinápticos de uma RNA consiste em compilar um conjunto de dados que relacionam as entradas e saídas do sistema em questão. Este procedimento é também conhecido como processo de treinamento e deve ser assegurado que a estrutura neural é exposta à seqüência de padrões que representam o comportamento do sistema analisado.
No sentido de gerar padrões de treinamento para a estimativa de conjugado foi desenvolvido o modelo matemático do motor de indução baseado na ferramenta computacional Matlab/Simulink®(Ong, 1997). Este modelo é aceito como representativo da realidade física do motor por diversos pesquisadores (Lixin e Rahman, 2001; Soares e Branco, 2001; Skibinski et. al., 1998; Pankau et. al., 1999) o qual leva em consideração vários aspectos envolvidos com a dinâmica eletromecânica do motor, permitindo a análise do comportamento do regime transitório ao regime permanente. Cabe salientar que a modelagem do MIT apresentado em Fitzgerald (1975), por exemplo, o qual é apresentado em diversos cursos de graduação, trata o modelo do MIT como um circuito equivalente válido para o regime permanente.
As principais não linearidades consideradas nas simulações foram o efeito pelicular (skin effect) e saturação. O efeito skin é maximizado durante o transitório e a saturação magnética tem relação direta com a corrente (Goedtel, 2003). Quando a corrente apresenta valores superiores à corrente nominal a curva de magnetização passa de uma região linear para uma região saturada (Ong, 1997; Goedtel, 2003). Devido ao curto espaço de tempo da simulação o efeito da temperatura não foi considerado nas simulações.
O diagrama esquemático representando as entradas e saídas do modelo são apresentados na figura 1. Os parâmetros da máquina, tais como tensão, parâmetros elétricos do rotor e estator, inércia da carga e do rotor, são as entradas do modelo. A corrente elétrica, o torque eletromagnético e velocidade do rotor são as saídas do modelo do MIT. Estas variáveis serão usadas no processo de treinamento da rede neural.

O diagrama esquemático apresentado na figura 1, usado para obtenção dos padrões de treinamento, é aplicado a todos os motores de indução trifásicos. Uma análise detalhada e aprofundada de todos procedimentos envolvidos com a modelagem e metodologia utilizada para geração dos vetores de dados de entrada/saída é apresentada em Goedtel (2003), sendo os mesmos capazes de gerar dados de forma precisa do regime transitório ao regime permanente. As não-linearidades expressas no conjunto de equações implementadas exigem longas simulações numa plataforma computacional baseada em PC, sendo que este fato inviabiliza a implementação em sistemas de tempo real.
A Tabela 1 mostra os parâmetros usados na simulação do MIT. Estes dados foram inseridos no algoritmo computacional representado através do diagrama em blocos da figura 1, gerando dados suficientes para o treinamento das redes neurais.

3 IDENTIFICAÇÃO ATRAVÉS DE REDES NEURAIS ARTIFICIAIS
A identificação de sistemas através das redes neurais artificiais tem mostrado resultados promissores na área de sistemas de potência. Mais especificamente, o uso de RNA tem oferecido esquemas alternativos ao tratamento de problemas relacionados às máquinas elétricas (Campbell e Summer, 2002; Kolla e Varatharasa, 2000; Kukolj et. al., 2000; Orille e Sowilam, 1999; Goedtel et. al., 2004b, Bharadwaj et. al., 2004). No presente trabalho, as RNA foram usadas para estimativa do conjugado da carga aplicada ao eixo do motor de indução.
Para a especificação correta de um motor de indução são necessárias informações da carga e da instalação, tais como: tensão de alimentação, rotação, altitude, regime de operação, conjugado de carga, entre outros, conforme descrito na NBR7094:1996. Destes parâmetros, o conjugado de carga é a variável que na maioria dos casos é desconhecida. A falta desta informação é compensada pelo seguinte procedimento: um motor é escolhido para determinada aplicação e, após o acionamento, mede-se a corrente e a velocidade. Se estas variáveis estiverem fora da faixa de operação nominal do motor este será substituído por outro, normalmente, de maior potência. Na maioria dos casos, do acompanhamento prático em diversos setores produtivos, apenas a corrente é medida uma vez que esta pode ser efetuada com um alicate amperométrico de baixo custo.
O objetivo primal deste trabalho é a estimativa de conjugado de carga aplicado ao eixo do motor de indução. Neste trabalho usou-se uma rede Perceptron multicamada com treinamento supervisionado. O algoritmo de treinamento tem dois passos básicos: o primeiro, chamado propagação, aplica valores às entradas da RNA e verifica a resposta. O valor da camada de saída é comparado com o valor desejado na saída. O segundo passo ocorre no sentido inverso, ou seja, da camada de saída para a entrada. O erro produzido na saída da rede é usado no processo de ajuste dos seus parâmetros internos (pesos e limiares), conforme demonstrado em Haykin (1999). O elemento básico de uma RNA é o neurônio artificial, também conhecido como elemento de processamento (Figura 2).

O modelo do neurônio artificial ilustrado na figura 2 pode ser equacionado da seguinte forma:


n é o número de sinais de entrada do neurônio.Xi é o i-ésimo sinal de entrada do neurônio.wi é o peso associado com o i-ésimo sinal de entrada.b é o limiar de cada neurônio.vj(k) é a resposta ponderada do j-ésimo neurônio em relação ao instante k.jj(.) é a função de ativação do j-ésimo neurônio.yj(k) é o sinal de saída do j-ésimo neurônio em relação ao instante k.
Cada neurônio artificial é capaz de computar os sinais de entrada e a respectiva saída. A função de ativação usada para calcular o sinal de saída é tipicamente não-linear. As RNA que processam dados analógicos, que estão envolvidas nesta aplicação, têm como função de ativação a sigmóide ou a tangente hiperbólica. O processo de ajuste dos pesos da rede wj associados ao j-ésimo neurônio de saída é feito pelo cálculo do sinal de erro em relação à k-ésima iteração ou ao k-ésimo vetor de entrada. Este sinal de erro é calculado pela seguinte equação:

onde dj(k) é a resposta desejada do j-ésimo neurônio de saída. Somando todos os erros quadráticos produzidos pelos neurônios de saída da rede em relação à k-ésima iteração, tem-se:

onde p é o número de neurônios da saída. Para uma configuração de pesos ótima, E(k) é minimizado pelo ajuste dos pesos sinápticos wji. Os pesos associados à camada de saída da rede são recalculados usando a seguinte expressão:

onde wji é o peso conectando o j-ésimo neurônio da camada de saída ao i-ésimo neurônio da camada anterior e h é a constante que determina a taxa de aprendizado do algoritmo de retro-propagação. O ajuste dos pesos pertencentes às camadas escondidas é feito de forma análoga. Os passos para o ajuste destes pesos são detalhados em Haykin (1999).
4 METODOLOGIA E SIMULAÇÃO
As pesquisas da CEMIG e COPEL, mencionadas na introdução, mostram o problema do dimensionamento dos motores nas regiões de atuação dessas empresas. Os procedimentos empíricos no projeto de uma máquina, a falta de uma função de transferência que modele a relação entre os diversos componentes, principalmente a energia de entrada e saída do processo, são alguns dos fatores que tornam a escolha de um motor elétrico um processo de tentativa e erro. O erro na escolha do motor mais adequado implica em redução da vida útil do mesmo - no caso subdimensionado - ou perdas de energia elétrica nos casos de superdimensionamento. Fornecer uma ferramenta alternativa para a escolha do motor elétrico mais adequado através da estimativa de conjugado de carga é a principal motivação desse trabalho. A figura 3 ilustra a metodologia aplicada na forma de diagrama em blocos.

As cargas industriais são classificadas, conforme Dias e Lobosco (1988) em seis grandes grupos e são descritas nas subseções a seguir. Para o estudo aqui desenvolvido serão considerados apenas quatro tipos de cargas que são as mais encontradas em aplicações industriais, ou sejam, a carga quadrática, a linear, a inversa e a constante. A Tabela 2 descreve estas cargas como funções matemáticas.

Para cargas lineares e quadráticas, a constante K está relacionada com o conjugado inicial em wt = 0+ . Em relação à carga constante o valor de K permanece inalterado durante a simulação. Para cargas inversas o valor de K representa o conjugado em regime permanente, ou seja wt = ¥.
À medida que aumenta a velocidade, as cargas quadrática e linear oferecem um maior conjugado de carga ao motor em todo o período transitório. Quando o conjugado de carga T(w) somado ao conjugado de perdas (por exemplo, atrito e ventilação) se iguala ao conjugado fornecido pelo motor - conjugado eletromagnético - o motor entra em regime permanente. A carga inversa, por sua vez, produz um efeito oposto às cargas linear e quadrática, pois com o incremento de velocidade, no regime transitório, T(w) diminui seu valor. A carga constante apresenta T(w) constante no regime transitório e no regime permanente.
Desta forma, a abordagem deste trabalho pode contribuir para sistemas de controle de alto desempenho, uma vez que leva em consideração o conjugado de carga no regime transitório e no regime permanente conforme as equações definidas na Tabela 2. De acordo com os trabalhos de Marino et. al. (2004) e Murat et. al. (2004), o conhecimento do conjugado de carga é uma necessidade dos controles de alto desempenho, onde a aplicação da metodologia proposta neste trabalho para fins de controle é uma perspectiva promissora de pesquisa em trabalhos futuros.
O conjugado de aceleração é aquele calculado pela diferença entre o conjugado oferecido pelo motor e os conjugados que se opõem ao conjugado motor. Para que o acionamento seja estável a taxa de variação do conjugado motor em relação à velocidade deve ser superior à taxa de variação do conjugado resistente em relação à velocidade do motor (Dias e Lobosco, 1988; pp. 34-37). Conhecendo-se então o comportamento do conjugado de carga, o qual é a maior parcela do conjugado resistente, é possível determinar o melhor método de partida para um determinado motor.
O momento de inércia é a segunda variável mecânica de suma importância para o dimensionamento do motor elétrico. Da mesma forma que o conjugado, o dado relativo a esta variável raramente é fornecido ao projetista da parte elétrica de máquinas e equipamentos.
O valor máximo de momento de inércia admitido em cargas acionadas por MIT é normalizado pela NBR 7094:1996 (Seção 6 e Tabela 3). Nas notas explicativas da seção é definida uma equação para valores de potências intermediárias de motores que não se encontram tabelados. Calculando-se o momento de inércia através da Equação (6) para alguns valores amostrais tabelados, obtém-se como resultado valores próximos dos apresentados na norma, subtraídos pequenos arredondamentos.

onde:
J é o momento de inércia medido em kgm2.Pn é a potência nominal do motor em kW.p é o número de pares de pólos.

Conforme mencionado acima em Dias e Lobosco (1988), o desconhecimento do momento de inércia da carga é um dos fatores que leva ao incorreto dimensionamento do motor elétrico.
Nesse trabalho o momento de inércia será considerado no modelo matemático do motor de indução e nas várias simulações que serão descritas. Optou-se por fazer um escalonamento linear do momento de inércia de um valor mínimo ao valor máximo (permitido pela norma) conforme o conjugado exigido pela carga, uma vez que não foram encontradas referências na literatura pesquisada no que tange o escalonamento do momento de inércia em simulações matemáticas. Desta forma, este trabalho também contribui para o estudo da modelagem e simulação do motor de indução.
O valor mínimo do momento de inércia, associado ao motor girando praticamente a vazio, é o valor do momento de inércia do rotor fornecido pelo fabricante do motor. Já o valor máximo de momento de inércia é calculado pela Equação (6), ou pela consulta à NBR7094:1996 (Tabela 3 e Seção 6), e está relacionado com o conjugado máximo exigido no eixo do motor.
A simulação do modelo do MIT descrito na Seção 2 produziu os dados necessários ao treinamento da RNA. Os dados de entrada da rede perceptron multicamada são a velocidade do motor, a corrente e a tensão de alimentação eficaz. A saída é o conjugado de carga conforme descrito na figura 4.

A figura 5 mostra, a título de exemplificação, a simulação de uma carga linear. Na simulação da carga quadrática, a qual é muito parecida com a carga linear, substituem-se às retas por parábolas. Na região limitada pelas curvas C1 a C26 a RNA faz a estimativa de conjugado.

A figura 6 mostra a simulação de uma carga constante limitada pelas curvas C1 a C26. A carga inversa tem a mesma região mapeada nas curvas, que neste caso, são exponenciais.

É importante notar que o mapeamento produz valores diferentes de conjugado (partida e regime permanente) para cada curva, dependendo do valor de tensão usado na alimentação do motor, conforme interseção das curvas de mapeamento e conjugado do motor (Fitzgerald et. al., 1975; Kosov, 1972; Goedtel, 2003).
Com a pesquisa à norma NBR7094:1996 e NBR5410:1999 optou-se, nesse trabalho, pela variação de tensão de -10% a +10% da tensão nominal conforme NBR7094:1996. Considerando a alimentação do motor em 220V, a faixa de tensão abordada na simulação compreende 198V a 242V. É de fundamental importância considerar esta variação na alimentação, pois o conjugado entregue a carga tem uma relação quadrática com a tensão de alimentação, conforme citado em Fitzgerald et. al. (1975), ou seja, "O conjugado interno desenvolvido por um motor é proporcional ao quadrado da tensão aplicada a seus terminais primários".
Utilizando a variação de tensão de alimentação no intervalo de -10% a +10% do valor nominal com passos de 2% para cada faixa obtém-se 11 zonas discretas para mapeamento do conjugado. O número total de simulações para cada carga é o produto do número de zonas pelo número de curvas, ou seja, para cada faixa de tensão foram gerados 26 conjuntos de dados, totalizando 286 simulações para cada carga.
4.1 Treinamento das Redes Perceptron Considerando Diferenças de Carga e Tensão de Alimentação
O treinamento da rede perceptron foi dividido conforme a característica de carga e por faixa de tensão dentro de cada conjunto de carga. A figura 7 ilustra essa divisão no formato de diagrama em blocos proposta por Goedtel (2003).

Um exemplo ilustrativo, no caso da carga quadrática e uma faixa de tensão (198V,...,242V), 26 curvas de simulação foram geradas. Estas curvas simularam o conjugado de carga de 5% a 250% do conjugado nominal, onde 13 curvas foram usadas para o treinamento da rede e 13 curvas diferentes usadas no processo de validação da rede. Cada conjunto de treinamento, composto por 13 curvas, é constituído por um conjunto de 100 dados de entradas-saída, os quais são arranjados de forma matricial. Cada faixa de tensão e tipo de carga possui uma rede neural específica descrito na figura 7como Rede 1 à Rede 11.
Após o processo de treinamento, a rede é capaz de estimar o conjugado de carga a partir de valores seqüenciais de tensão, corrente e velocidade. O procedimento de validação baseou-se no uso de padrões de dados não utilizados no treinamento.
Para as cargas linear, quadrática e inversa houve resultados de generalização satisfatórios com a estrutura neural tendo 5 neurônios na primeira camada oculta, 25 neurônios na segunda camada oculta e um neurônio na camada de saída. A estrutura neural para a carga constante obteve resultados de generalização como uma estrutura neural menor que as anteriores, sendo composta por 5 neurônios na primeira camada oculta, 15 neurônios na segunda camada e um neurônio na saída. As funções de ativação em todos os casos foram a tangente hiperbólica nas camadas ocultas e linear para a saída.
O método utilizado para determinar a melhor topologia de rede para cada uma das cargas foi aquele baseado na técnica cross-validation (Haykin, 1999), a qual permite identificar de forma apropriada o número de camadas e o número de neurônios (por camada) a serem utilizados em cada estrutura neural.
5 RESULTADOS DE SIMULAÇÃO
Esta seção apresenta as diversas simulações desenvolvidas neste trabalho. Cabe salientar que os dados mostrados à rede não fizeram parte do treinamento delas. Demonstra-se dessa forma a capacidade de generalização das redes neurais artificiais. Em todas as simulações apresentadas nesse capítulo o período de simulação é de 5 segundos e o período de amostragem de 1.10 - 1s.
Na apresentação dos resultados a seguir há duas curvas em cada gráfico. Uma curva é a do conjugado de carga apresentado ao MIT (Tabela 2) através da simulação das funções matemáticas e, a outra curva, é a produzida pela saída da rede neural artificial com dados de tensão, corrente e velocidade gerados também pela simulação do modelo do MIT. A diferença entre as duas curvas, conjugado desejado e conjugado estimado, gera o erro descrito nas Tabelas 3 a 6.
Deve ser salientado que as análises sobre dimensionamento levam em consideração o conjugado exigido pela carga no eixo do motor de 1 hp, o qual tem conjugado nominal de 4,1 Nm.
5.1 Carga Quadrática
No treinamento da carga quadrática foram utilizadas 26 curvas que simularam da partida ao regime permanente o comportamento de um MIT submetido a esse tipo de carga, para cada faixa de tensão. Dessas curvas 13 foram usadas no treinamento e as outras 13 usadas no teste de validação da rede. Gera-se, desta forma, uma RNA para cada faixa de tensão.
A figura 8 mostra o resultado de generalização para a carga quadrática com conjugado inicial em 0,5 Nm e regime permanente em 150% do conjugado nominal. Esse motor opera subdimensionado e sua vida útil é comprometida.

A figura 9 mostra os resultados da simulação do MIT submetido ao conjugado quadrático alimentado em 215V. No caso da verificação do dimensionamento do MIT, apesar do erro entre as duas curvas ser da ordem de 5%, pode-se dizer que o motor submetido a este ensaio está bem dimensionado.

A figura 10 mostra o ensaio hipotético de um motor, submetido ao mesmo tipo de carga - quadrático - mas que em regime permanente exige 2,5 Nm. Neste caso, analisando apenas o conjugado de carga, é sugerida a troca desse motor de 1 cv por outro de 0,75 cv cujo conjugado nominal é de 3,1 Nm conforme o catálogo de motores de um fabricante nacional. A figura 11representa o ensaio de um motor que exige 5% do conjugado nominal com grandes perdas de rendimento e aumento do fator de potência.


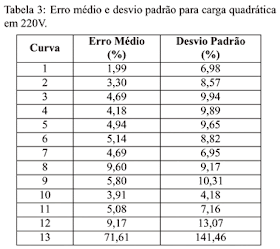
A Tabela 3 mostra o erro relativo médio e desvio padrão das curvas utilizadas na validação da rede perceptron para a tensão de 220V.
A décima terceira curva apresenta erro bem acima das demais. Este erro está relacionado com a curva da figura 11, onde o conjugado exigido no eixo é de 5% do valor nominal do motor. Pode-se inferir que a rede possui boa capacidade de generalização (erro < 10%) com valores de conjugado acima de 10% do conjugado nominal até 250% do mesmo. Se comparado a um torquímetro, pode-se fazer uma analogia com a sensibilidade mínima do instrumento, ou seja, o menor valor a ser medido dentro da faixa de erro esperada.
Para os propósitos desse trabalho, apesar da pouca precisão nessa última medida, pode-se julgar que o motor ensaiado está superdimensionado.
5.2 Carga Linear
No treinamento da carga linear, da mesma forma que a carga anterior, foram utilizadas 26 curvas que simulam da partida ao regime permanente o comportamento de um MIT submetido a esse tipo de carga para cada faixa de tensão. Dessas curvas 13 foram usadas no treinamento e as outras 13 usadas no teste de validação da rede, uma para cada faixa de tensão.
A figura 12 mostra os resultados da simulação de uma carga linear que, em regime permanente, atinge 180% do conjugado nominal do motor. Nesse caso sugere-se a troca do motor por outro de 2 cv cujo conjugado nominal é de 8,3 Nm conforme tabela de fabricante nacional.

A figura 13 mostra os ensaios de um motor alimentado com 215V submetido a um conjugado linear de aproximadamente 85% de seu conjugado nominal em regime permanente. Considera-se esse motor, sob o ponto de vista do conjugado exigido, bem dimensionado.

A figura 14 mostra um motor alimentado com sobretensão de 242V e com conjugado em regime permanente de aproximadamente 40% do conjugado nominal do motor. Sugere-se, nesse caso simulado, a troca do motor por outro de 4 pólos e 0,5 cv cujo conjugado nominal é de 2,07 Nm.

A figura 15 mostra a simulação de um motor alimentado com 198V e conjugado em regime permanente de aproximadamente 4 Nm. Entretanto, pela subtensão aplicada na alimentação, pode-se trabalhar de forma subdimensionada ou superdimensionada. A exemplificação é ilustrada na figura 16.


Considerando as curvas C1 e C2 que representam a simulação de duas cargas lineares, a carga C1mostra que está bem dimensionada mesmo com subtensão já que as curvas de conjugado do motor para as várias tensões são as mesmas na região de interseção com C1 (ponto Crp1). Ao contrário, a curva C2 apresenta três pontos de interseção, uma para cada tensão. O ponto Crp2, originário da interseção da curva em 198V, se analisado apenas sob a ótica do conjugado em regime permanente, poder-se-ia dizer que o motor está bem dimensionado.
Essa afirmação está incorreta para a curva C2 já que a velocidade em regime seria de aproximadamente 20% do valor síncrono e as correntes num valor próximo ao valor de partida. Para a mesma curva em questão, a análise dos pontos Crp3 e Crp4 demonstra que o motor está subdimensionado. Dessa forma deve-se ter cuidado nas afirmações quando uma subtensão é aplicada numa análise que considera apenas o conjugado em regime permanente. Nesse caso a análise do valor da corrente em regime seria "a prova real" para a questão.
Da mesma forma que na carga quadrática, o maior erro da carga linear é para valores de conjugado de carga inferiores a 10% do conjugado nominal do motor (curvas 12 e 13). Mesmo com esse erro é possível inferir que o motor de 1 cv encontra-se superdimensionado e sua troca tornar-se-á necessária. Perde-se credibilidade nessa faixa de 0 a 10% do conjugado nominal pelo erro apresentado, pois não é possível estimar o conjugado da carga dentro de uma faixa de erro aceitável. Ainda assim, prediz-se o problema de dimensionamento.
Nesse caso, após essa análise preliminar se pode substituir o motor na aplicação por outro, refazer o ensaio e apresentar-se o novo conjunto de dados a outra rede, treinada para o novo motor que por sua vez é de menor potência, e que responderia de forma adequada. É um processo interativo quando o conjugado exigido no eixo, nesse primeiro motor, fica abaixo dos valores esperados de 10% do conjugado nominal.
A Tabela 4 mostra os valores do erro relativo médio e desvio padrão para as simulações das cargas lineares.

5.3 Carga Constante
No treinamento da carga constante foram utilizadas 20 curvas que simulam da partida ao regime permanente o comportamento de um MIT submetido à carga constante para cada faixa de tensão. Destas curvas 10 foram usadas no treinamento e as outras 10 usadas no teste de validação da rede. O procedimento foi repetido para cada faixa de tensão.
As simulações com as funções matemáticas que exigiam maior conjugado quando submetidas às tensões abaixo da nominal apresentaram problemas de partida. Dessa forma o conjunto de treinamento foi reduzido. As simulações variaram de 5% do conjugado nominal a 150%.
A carga constante, por sua vez, apresentou problemas de convergência no algoritmo de treinamento. De uma forma geral as RNAs apresentam esses problemas quando as entradas ou saídas são associadas a valores constantes.
De forma simplificada a rede "não entende" como há variação nas entradas ou saídas enquanto um dos valores permanece constante. A primeira abordagem leva ao descarte desta variável, pois o sistema apresenta-se independente dela. Entretanto, no caso desse trabalho, a saída é o valor que a rede deve estimar. Há mudança nas três variáveis de entrada, quais sejam: tensão, corrente e velocidade enquanto a saída permanece inalterada.
A solução encontrada para essa questão foi somar um sinal senoidal à variável de saída da rede, antes do treinamento, de frequência 1 rad/s e amplitude menor que 5% do valor do conjugado. O problema de convergência numérica do algoritmo foi prontamente eliminado. Quando o teste de generalização foi realizado, mostrando à rede sinais de entrada diferentes daqueles do treinamento, há na saída o sinal senoidal introduzido no treinamento. Nesse ponto existem duas opções: i) sendo o sinal introduzido no treinamento de freqüência conhecida é possível introduzir um filtro para retirada do sinal do resultado de generalização, e ii) deixar o sinal cuja amplitude não ultrapassa o valor de 5% do valor constante esperado e levar este fato em consideração na análise dos dados. Nesse trabalho optou-se pela segunda alternativa, deixando o valor periódico como poderá ser visto nos resultados da próxima seção.
Esse procedimento é similar à técnica de multiplexação por divisão em frequência utilizada em telecomunicações. Nessa técnica vários sinais são somados, com frequências diferentes, e transmitidos num canal comum de comunicação. Na saída aplica-se um filtro para cada frequência utilizada na transmissão (Gibson, 1993). Entretanto, o uso desta metodologia foi modificada e utilizada em Goedtel (2003) no treinamento das RNA e o aprofundamento matemático apresentado em Goedtel et. al. (2004a).
Conforme descrito em Goedtel (2003), soma-se um sinal periódico a outro constante (de freqüência nula) no treinamento da rede. Dessa forma o sinal periódico aparece nos testes de generalização e pode ser filtrado. A amplitude do sinal periódico utilizado foi de 5% do conjugado de carga e a freqüência do sinal periódico foi de 1 rad/s.
O procedimento empregado traduz em uma contribuição à solução de problemas de convergência numérica encontrados em redes neurais artificiais. Foram utilizados cinco neurônios na primeira camada oculta, quinze na segunda camada oculta e um na saída. A estrutura é ligeiramente diferente das redes anteriores, mas o erro objetivado no treinamento (5.10 - 3), bem como o número máximo de épocas de treinamento, permanecem inalterados.
A figura 17 mostra o resultado de simulação para um motor de 1 cv alimentado com 198V e conjugado constante de 6,5 Nm.
Esse motor apresenta-se subdimensionado e sugere-se a troca do mesmo por outro de 1,5 cv cujo conjugado nominal é de 6,3 Nm.
Esse motor apresenta-se subdimensionado e sugere-se a troca do mesmo por outro de 1,5 cv cujo conjugado nominal é de 6,3 Nm.

A figura 18 mostra a simulação de um motor alimentado com 211V e conjugado constante de 95% do conjugado nominal.

A figura 19 apresenta o resultado de generalização de uma carga constante acoplada a um MIT de 1cv e alimentado com 220V.

A figura 20 ilustra um motor com problema de dimensionamento, pois a estimativa mostrou um valor entre 0,3 Nm e 0,4 Nm, bem abaixo da capacidade nominal do motor.

O sinal de erro quase periódico é resultado da inserção de um sinal senoidal de amplitude de 5% do conjugado de treinamento e frequência de 1 rad/s. Convém lembrar que os dados usados nos testes aqui não foram usados no treinamento, reforçando assim a idéia de que a rede "aprendeu" o padrão apresentado.

Seguindo o padrão de erro das cargas anteriores o pior resultado é encontrado na faixa de até 10% do conjugado nominal. A figura 20 mostra-se um bom exemplo. Pela análise qualitativa da curva é possível determinar a natureza da carga acionada (praticamente constante), bem como o mau dimensionamento do motor. Cabe salientar que a décima primeira curva de teste foi usada no treinamento.
5.4 Carga Inversa
No treinamento da carga inversa foram utilizadas 14 curvas que simulam da partida ao regime permanente o comportamento de um MIT submetido à carga inversa para cada faixa de tensão. Destas curvas 7 foram usadas no treinamento e as outras 7 usadas no teste de validação da rede. O procedimento foi reptido para cada faixa de tensão.
Da mesma forma que na carga constante a simulação dessa carga apresentou problemas de partida com o menor valor de tensão, ou seja, 198V. Seguindo o mesmo procedimento da carga constante escolheu-se iniciar a simulação em 150% do conjugado nominal para wt = 0 + , quando alimentado com tensão inferior à nominal. Seguindo o procedimento das cargas anteriores, os resultados de simulação foram usados para treinar a rede perceptron. Outras simulações, com outros parâmetros na função matemática que descreve a carga, foram usadas para testar a generalização da rede como descrito nas figuras 21 a 23.



A figura 21 mostra uma carga com 140% do conjugado nominal na partida e reduzindo seu valor à medida que há o incremento de velocidade. A partir deste gráfico observa-se que essa carga tende assintoticamente a 2,0 Nm.
A figura 22 mostra a simulação de um motor alimentado em 220V com conjugado de partida de 170% do conjugado nominal e em regime a um valor muito próximo do conjugado nominal. Pode-se considerar igualmente bem dimensionado o motor. Apenas uma ressalva deve ser feita, ou seja, no caso de haver subtensão na rede de alimentação esta máquina poderá apresentar problemas de partida. Nesses casos, o motor é normalmente substituído por outro de potência superior.
A figura 23 mostra um caso típico de superdimensionamento. O conjugado de partida exigido é de aproximadamente 4,6 Nm estimado e de 4,8 Nm simulado. Em regime permanente o conjugado exigido é de 1,5 Nm. Para análise desse caso, levando em consideração apenas o conjugado de partida e regime, sugere-se a substituição do motor de 1 cv por outro de 0,5 cv cujo conjugado nominal é de 2,1 Nm e a relação entre conjugado de partida pelo nominal é de 2,7 vezes (5,7 Nm).
A figura 24, seguindo o padrão das outras simulações, tem o maior erro no valor de conjugado em regime permanente, o qual estima o conjugado do MIT na faixa de 5% do nominal.

A Tabela 6 mostra os valores do erro relativo médio e desvio padrão para as simulações da carga inversa para a faixa de tensão de 220 V.

Confirmando o padrão das demais simulações, a faixa de conjugado, em regime permanente, inferior a 10% do conjugado nominal apresenta o maior erro. Como em um instrumento de medida, a rede neural também apresenta suas limitações no mapeamento de conjugado. Ainda assim, é possível atestar o dimensionamento do motor e, para a diminuição do erro, sugere-se um processo interativo, qual seja, substituir o motor por outro de menor potência no processo (ou máquina) e coletar os dados mostrando-os a outra rede, treinada para o novo motor.
6 CONCLUSÃO
Os resultados de simulação confirmam que é possível estimar o conjugado exigido no eixo de um motor de indução trifásico usando redes neurais artificiais. As entradas do sistema são medidas de tensão, corrente e velocidade com a capacidade de estimar o conjugado exigido no eixo do MIT. A estimativa abrange a faixa de 10% do conjugado nominal do motor até 150% do conjugado nominal (nos casos de conjugado inicial maior que zero) e estima-se até 250% de conjugado em regime permanente para conjugado inicial próximo de zero (em torno de 5% do valor nominal). A metodologia usada neste trabalho pode ser aplicada em outras cargas e tipos de motores.
O método desenvolvido neste estudo pode ser usado como uma ferramenta alternativa na identificação do comportamento da carga acoplada ao eixo do motor de indução e auxiliar o projetista na tarefa de escolha do melhor motor para uma aplicação específica.
Outra vantagem deste método é a ausência de parâmetros elétricos e mecânicos do motor após o treinamento da rede, uma vez que os referidos parâmetros são implícitos nos pesos da rede.
As principais justificativas para o uso destas técnicas são as seguintes: i) a estimativa de conjugado é feita diretamente por uma rede neural artificial, ii) o método pode ser usado como uma ferramenta auxiliar no dimensionamento e controle do motor de indução, iii) o método avalia se um motor está subdimensionado ou superdimensionado em uma aplicação específica, iv) a proposta apresentada exige apenas medidas de variáveis primárias na máquinas, tais como tensão, corrente e velocidade, v) a implementação desta metodologia pode ser feita através de hardware ou software.
Deve ser destacado que a metodologia desenvolvida neste trabalho se aplicada a diversos setores produtivos, pode contribuir de forma significativa para a redução das perdas de energia elétrica, as quais são pertinentes ao mau dimensionamento do motor de indução.
A medida de velocidade é uma das variáveis de entrada do sistema proposto neste trabalho. Há métodos de estimadores que podem substituir a medida direta desta variável. As principais metodologias de estimadores de velocidade empregadas originam-se em estimadores de malha aberta com monitoramento de corrente e tensão do estator, observadores de estado, sistemas de referência com modelos adaptativos e estimadores baseados em inteligência artificial. As técnicas de inteligência artificial advêm principalmente das redes neurais artificiais e lógica fuzzy (Vas, 1998). Estimadores de velocidade baseados em redes neurais artificiais foram prospostas também por Goedtel et. al. (2004b), onde o aperfeiçoamento destes modelos de estimadores é objeto de estudos futuros.
Finalmente, em aplicações industriais envolvendo processos de tempo real, a metodologia proposta tem excelente potencial para implementação em hardware usando processadores de DSP (Digital Signal Processing) ou FPGAs (Field Programable Gate Arrays), os quais podem ser integrados aos eficientes métodos de controle dos motores de indução nos regimes transitório e permanente.
AGRADECIMENTOS
Os autores agradecem à FAPESP (Processo nº 03/11353-0) pelo auxílio financeiro concedido e aos revisores pelas valiosas contribuições ao trabalho.
REFERÊNCIAS
Associação Brasileira de Normas Técnicas - ABNT (1996). NBR 7094: Máquinas Elétricas Girantes - Motores de Indução - Especificação. Rio de Janeiro. [ Links ]
Bharadwaj, R. M., Parlos, A. G., Toliyat, H. A. (2004). Neural speed filtering for sensorless induction motor drives. Control Engineering Practice, 12, pp. 687-706. [ Links ]
Boulter, B. T. (2004). Selecting the right drive. IEEE Industry Applications Magazine, July/August 2004, pp. 16-23. [ Links ]
Britto, R. M. (1994). Sistema Eletro-Eletrônico para Medição de Torque em Dispositivos Girantes Utilizando Extensômetro de Resistência Elétrica. Tese de Doutorado. Universidade Federal do Rio Grande do Sul (UFRGS/PPGEM). [ Links ]
Campbell, J., Summmer, M. (2002). Practical sensorless induction motor drive employing an artificial neural network for online parameter adaptation. IEE Proc. Electr. Power Appl., 149, pp. 255-260. [ Links ]
Chen, T. C., Sheu, T. T. (2002). Model reference neural network controller for induction motor speed control. IEEE Transactions on Energy Conversion, 17, pp. 157-163. [ Links ]
Dias, L. P. C., Lobosco, O. S. (1988). Motores Elétricos: Seleção e Aplicação. McGraw-Hill. [ Links ]
El-Ibiary, Y. (2003). An accurate low-cost method for determining electric motors' efficiency for the purpose of plant energy management. IEEE Transactions on Industry Applications, 39, pp.1205-1210. [ Links ]
Fitzgerald, A. E., Kingsley JR., Kusko, A. C. (1975). Electric Machinery. McGraw-Hill, [ Links ]
Gibson, J. D. (1993). Principles of Digital and Analog Communications. McMillan Inc. [ Links ]
Goedtel, A. (2003).
Goedtel, A., Silva, I. N., Serni, P. J. A. (2004a). An alternative approach to solve convergence problems in the backpropagation algorithm. IEEE International Joint Conference on Neural Networks (IJCNN2004), pp. 1021-1026. [ Links ]
Goedtel, A., Silva, I. N., Serni, P. J. A. (2004b). Speed estimation in induction motors using artificial neural networks. 11TH IFAC Symposium on Information Control Problems in Manufacturing (INCOM2004), CD-ROM, Artigo no. 48. [ Links ]
Haykin, S. (1999). Neural Networks - A Comprehensive Foundation. Prentice-Hall. [ Links ]
Huang, C. Y., Chen, T. C., Huang, C. L. (1999). Robust control of induction motor with a neural-network load torque estimator and a neural-network identification. IEEE Transactions on Industrial Electronics, 46, pp. 990-997. [ Links ]
Kolla, S., Varatharasa, L. (2000). Identifying three-phase induction motor faults using artificial neural networks. ISA Transactions, 39, pp. 433-439. [ Links ]
Kosov, I. L. Electrical Machinery and Transformers. Prentice-Hall, Inc., 1972. [ Links ]
Krzeminski, Z. (1999). A new speed observer for control system of induction motor. Proceedings of IEEE International Conference on Power Electronics and Drive Systems, pp. 555-560. [ Links ]
Kukolj, D., Kulic, F., Levi, E. (2000). Design of speed controller for sensorless electric drives based on AI techniques: a comparative study. Artificial Intelligence in Engineering, 14, pp. 165-174. [ Links ]
Lin, F. J., Way, R. J. (2002). Adaptive fuzzy-neural-network control for induction spindle motor drive. IEEE Transactions on Energy Conversion, 17, pp. 507-513. [ Links ]
Lixin, T., Rahman, M. F. (2001) A new direct torque control strategy for flux and torque ripple reduction for induction motors drive - a Matlab/Simulink model. IEEE International Conference on Electric Machines and Drives, pp. 884-890. [ Links ]
Marach, L. C. (2001). Metodologia para determinar a substituição de motores superdimensionados. Revista Eletricidade Moderna, Agosto, pp. 220-228. [ Links ]
Marino, R., Tomei, P., Verreli, C. M. (2004). A global tracking control for speed-sensorless induction motors. Automatica, 40, pp. 1071-1077. [ Links ]
Murat, B., Bogosyan, S., Gosakan, M. (2004). Speed sensorless direct torque control of IMs with rotor resistance estimation. Energy Conversion and Management, Article in Press. [ Links ]
Narendra, K. S., Parthasarathy, K. (1990). Identification and control of dynamical systems using neural networks", IEEE Transactions on Neural Networks, 1, pp. 1-27. [ Links ]
Ong, C. M. (1997). Dynamic Simulation of Electric Machinery Using Matlab/Simulink. Prentice Hall, 1997. [ Links ]
Orille, A. L., Sowilam, G. M. A. (1999). Application of neural networks for direct torque control. Computers & Industrial Engineering, 37, pp. 391-394, 1999. [ Links ]
Pankau, J., Leggate, D., Schlegel, D.W., Kerkman, R. J., Skibinski, G. L. (1999). High-frequency modeling of current sensors. IEEE Transactions on Industry Applications, 35, pp. 1374-1382. [ Links ]
Proca, A. B., Keyhami, A., Miller, J. M. (2003). Sensorless sliding-mode control of induction motors using operating condition dependent model. IEEE Transactions on Energy Conversion, 18, pp. 205-212. [ Links ]
Sheu, T. T., Chen, T. C. (1999). Self-tuning control of induction motor drive using neural network identifier. IEEE Transactions on Energy Conversion, 14, pp. 881-886. [ Links ]
Skibinski, G. L., Kerkman, R. J., Leggate, D., Pankau, J., Schlegel, D. W. (1998). Reflected wave modeling techniques for PWM AC motor drives. Proceedings of 13th Annual Conference on Applied Power Electronics Conference, 2, pp. 1021-1029. [ Links ]
Soares, F., Branco, P. J. C. (2001). Simulation of a 6/4 switched reluctance motor based on Matlab/Simulink environment. IEEE Transactions on Aerospace and Electronic Systems, 37, pp. 989-1009. [ Links ]
Vas, P. (1998). Sensorless Vector and Indirect Torque Control. Oxford University Press. [ Links ]
Vas, P. (1999). Artificial Intelligence Based Electrical Machines and Drives, Oxford University Press. [ Links ]
Artigo submetido em 16/01/2005
1a. Revisão em 08/06/2006
2a. Revisão em 29/08/2006
1a. Revisão em 08/06/2006
2a. Revisão em 29/08/2006
Aceito sob recomendação do Editor Associado Prof. José Antenor Pomilio